单链表反转
思路
迭代:在遍历列表时,将当前节点的 next 指针改为指向前一个元素。由于节点没有引用其上一个节点,因此必须事先存储其前一个元素。在更改引用之前,还需要另一个指针来存储下一个节点。不要忘记在最后返回新的头引用!
复杂度分析
- 时间复杂度:O(n),假设 n 是列表的长度,时间复杂度是 O(n)。
- 空间复杂度:O(1)。
代码(Go)
//Definition for singly-linked list.
type ListNode struct {
Val int
Next *ListNode
}
func reverseList(head *ListNode) *ListNode {
var prev *ListNode = nil
curr := head
for curr != nil {
nextTemp := curr.Next
curr.Next = prev
prev = curr
curr = nextTemp
}
return prev
}
链表中环的检测
思路
通过使用具有 不同速度 的快、慢两个指针遍历链表,空间复杂度可以被降低至 O(1)。慢指针每次移动一步,而快指针每次移动两步。
如果列表中不存在环,最终快指针将会最先到达尾部,此时我们可以返回 false。
复杂度分析
-
时间复杂度:O(n),让我们将 n 设为链表中结点的总数。为了分析时间复杂度,我们分别考虑下面两种情况。
-
链表中不存在环: 快指针将会首先到达尾部,其时间取决于列表的长度,也就是 O(n)。
-
链表中存在环: 我们将慢指针的移动过程划分为两个阶段:非环部分与环形部分:
-
1.慢指针在走完非环部分阶段后将进入环形部分:此时,快指针已经进入环中 迭代次数=非环部分长度=N
-
2.两个指针都在环形区域中:考虑两个在环形赛道上的运动员 - 快跑者每次移动两步而慢跑者每次只移动一步。其速度的差值为 1,因此需要经过 速度差值/二者之间距离 次循环后,快跑者可以追上慢跑者。这个距离几乎就是 “环形部分长度 K” 且速度差值为 1,我们得出这样的结论 迭代次数=近似于 “环形部分长度 K”.
-
因此,在最糟糕的情形下,时间复杂度为 O(N+K),也就是 O(n)。
-
-
空间复杂度:O(1),我们只使用了慢指针和快指针两个结点,所以空间复杂度为 O(1)。
代码(Go)
//Definition for singly-linked list.
type ListNode struct {
Val int
Next *ListNode
}
func hasCycle(head *ListNode) bool {
if head == nil || head.Next == nil {
return false
}
slow := head
fast := head.Next
for slow != fast {
if fast == nil || fast.Next == nil {
return false
}
slow = slow.Next
fast = fast.Next.Next
}
return true
}
两个有序链表的合并
思路
首先,我们设定一个哨兵节点 “prehead” ,这可以在最后让我们比较容易地返回合并后的链表。我们维护一个 prev 指针,我们需要做的是调整它的 next 指针。然后,我们重复以下过程,直到 l1 或者 l2 指向了 null :如果 l1 当前位置的值小于等于 l2 ,我们就把 l1 的值接在 prev 节点的后面同时将 l1 指针往后移一个。否则,我们对 l2 做同样的操作。不管我们将哪一个元素接在了后面,我们都把 prev 向后移一个元素。
在循环终止的时候, l1 和 l2 至多有一个是非空的。由于输入的两个链表都是有序的,所以不管哪个链表是非空的,它包含的所有元素都比前面已经合并链表中的所有元素都要大。这意味着我们只需要简单地将非空链表接在合并链表的后面,并返回合并链表。
复杂度分析
-
时间复杂度:O(n + m) 。因为每次循环迭代中,l1 和 l2 只有一个元素会被放进合并链表中, for 循环的次数等于两个链表的总长度。所有其他工作都是常数级别的,所以总的时间复杂度是线性的。
-
空间复杂度:O(1) 。迭代的过程只会产生几个指针,所以它所需要的空间是常数级别的。
代码(Go)
//Definition for singly-linked list.
type ListNode struct {
Val int
Next *ListNode
}
func mergeTwoLists(l1 *ListNode, l2 *ListNode) *ListNode {
preHead := &ListNode{}
prev := preHead
for l1 != nil && l2 != nil {
if l1.Val <= l2.Val {
prev.Next = l1
l1 = l1.Next
}else {
prev.Next = l2
l2 = l2.Next
}
prev = prev.Next
}
if l1 == nil {
prev.Next = l2
}
if l2 == nil {
prev.Next = l1
}
return preHead.Next
}
删除链表倒数第n个结点
思路
我们可以使用两个指针而不是一个指针。第一个指针从列表的开头向前移动 n+1 步,而第二个指针将从列表的开头出发。现在,这两个指针被 n 个结点分开。我们通过同时移动两个指针向前来保持这个恒定的间隔,直到第一个指针到达最后一个结点。此时第二个指针将指向从最后一个结点数起的第 n 个结点。我们重新链接第二个指针所引用的结点的 next 指针指向该结点的下下个结点。
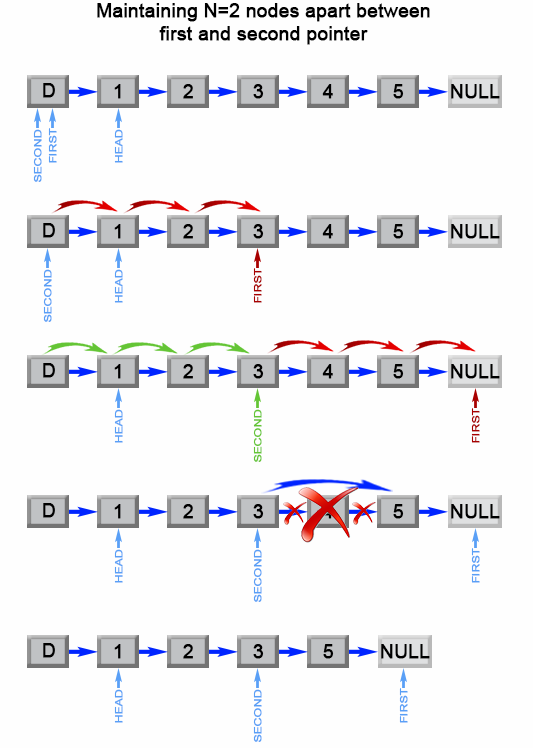
复杂度分析
-
时间复杂度:O(L),该算法对含有 L 个结点的列表进行了一次遍历。因此时间复杂度为 O(L)。
-
空间复杂度:O(1),我们只用了常量级的额外空间。
代码(Go)
//Definition for singly-linked list.
type ListNode struct {
Val int
Next *ListNode
}
func removeNthFromEnd(head *ListNode, n int) *ListNode {
var dummy = &ListNode{}
dummy.Next = head
first := dummy
second := dummy
for i := 1; i <= n + 1; i++ {
first = first.Next
}
for first != nil {
first = first.Next
second = second.Next
}
second.Next = second.Next.Next
return dummy.Next
}
求链表的中间结点
思路
用两个指针 slow 与 fast 一起遍历链表。slow 一次走一步,fast 一次走两步。那么当 fast 到达链表的末尾时,slow 必然位于中间。
复杂度分析
-
时间复杂度:O(N),其中 N 是给定链表的结点数目。
-
空间复杂度:O(1),只需要常数空间存放 slow 和 fast 两个指针。
代码(Go)
//Definition for singly-linked list.
type ListNode struct {
Val int
Next *ListNode
}
func middleNode(head *ListNode) *ListNode {
slow := head
fast := head
for fast != nil && fast.Next != nil {
slow = slow.Next
fast = fast.Next.Next
}
return slow
}