私钥
私钥就是一组随机获取的数字。
私钥用来生成数字签名,在交易中用于证明对以太币的所有权。私钥必须严格保密,也必须妥善保存,私钥丢失的话是无法找回的。
通过随机数生成私钥
私钥的生成就是在1到2256之间选择数字,更准确地说,以太坊私钥可以是任何比2256略微小一点的正整数,2256是一个77位的十进制数字,接近于1.158×1077。私钥的数字与2256的前38位相同,这被定义为以太坊椭圆曲线的阶(详见后面的椭圆密码学的基本概念)。要生成私钥,我们随机取出一个256比特的数字,然后检查它是否在有效范围内。用编程术语来说,其实现方式是:将一个(从密码学意义上安全的熵源中得出的)很大的随机字符串放入256比特的哈希算法(详见后面的密码学的哈希算法)中,比如Keccak-256或者SHA256,这两种算法会便捷地产生一个256比特的数字。如果这个结果在有效范围内,我们就有了一个合适的私钥。否则,我们就要用另一个随机数字再试一次。
privatekey = SHA256/Keccak-256("很大的随机字符串")
以太坊私钥数字区间大小为2256,这是一个大到无法言喻的数字。这个数字在十进制中几乎是1077,当你随机地选择了一个私钥后,几乎不可能会有另一个人猜到,或者选中同一个。
需要注意的是,私钥的生成是离线的,不会和网络或者任何人交互。密码学的随机数生成使用熵源充足的随机源做种子,可以保证两次选择的随机数不重复,既不可能被别人猜到。
下面就是一个随机生成的私钥,以十六进制表示(“256个二进制位,显示为64个十六进制数,每个代表4比特)。
f8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315
公钥
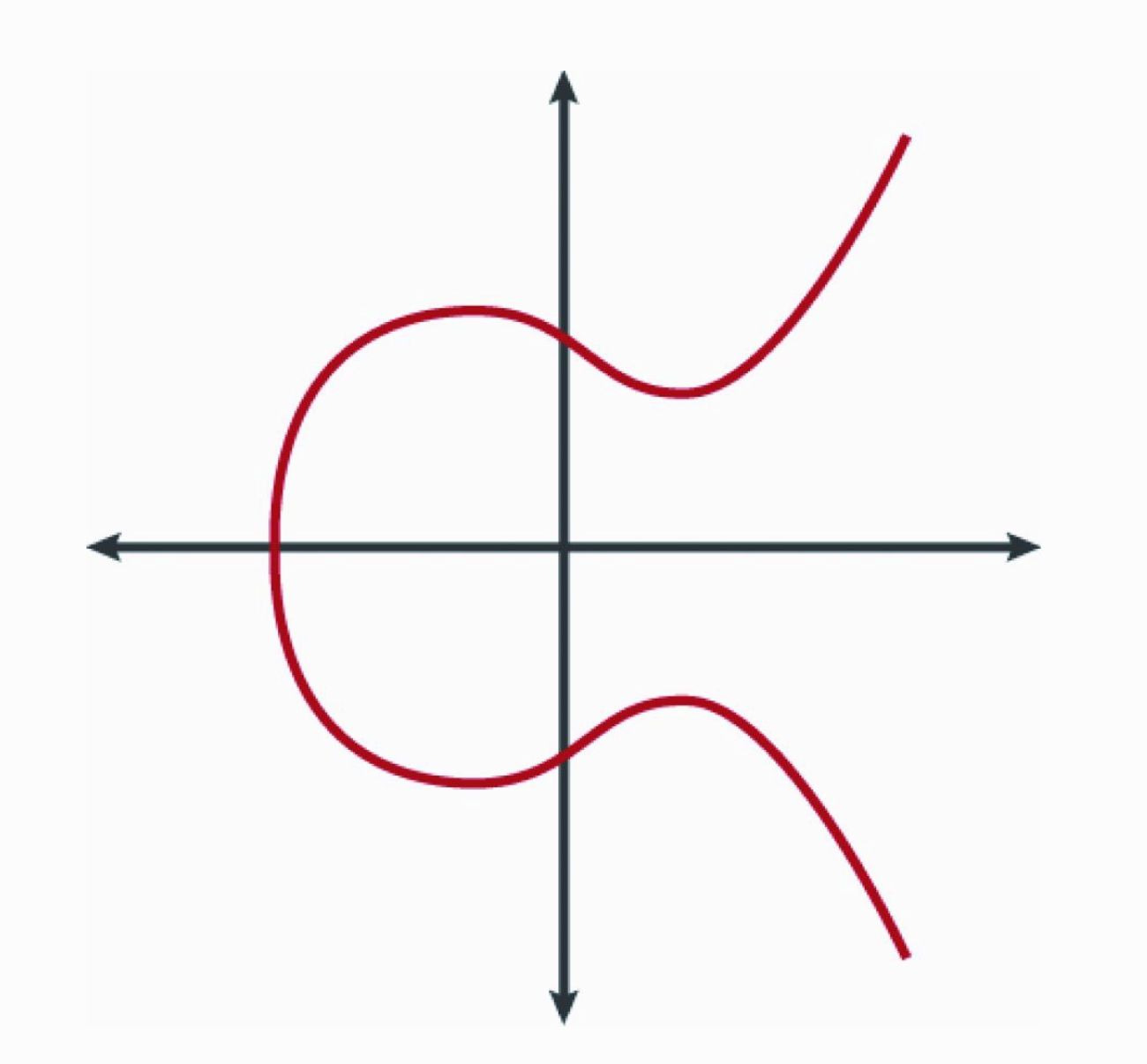
每个以太坊公钥都是椭圆曲线上的一个点,也就是说,每个公钥都是一组x、y坐标,这个坐标正好满足椭圆曲线方程。
公钥是通过对私钥使用椭圆曲线的乘法运算得来的,而这个乘法运算基本上是不可逆的:K=kG,其中k是私钥,G是一个常量点,称为生成点,K是计算得来的公钥,是椭圆曲线函数的乘法运算符号。这与普通乘法运算的规则是不同的,除了与普通乘法有相同的功能属性,其他都不一样。举个例子,反向运算(普通乘法的反向运算就是除法),也称为获取“离散对数”的计算,即在已知K的情况下求解k,是非常困难的,必须采用暴力穷举的方式尝试所有可能的k。 也就是说,椭圆曲线之上的算术运算跟常规的数学运算是不一样的。一个点(G)可以与一个整数(k)相乘来获得另外一个点(K)。但是椭圆曲线的世界里没有除法的概念。因此不可能简单地通过计算公钥K对G点的除法来计算私钥。
椭圆曲线乘法是“单向”函数:它很容易从一个方向(乘法)进行计算,但是不可能采用反向(除法)的方式计算。
私钥的持有者很容易算出公钥,然后把公钥公开,因为他确信没有人可以通过这个公钥反向推算出私钥。这个神奇的数学算“法造就了不可篡改和安全的数字签名,用来证明以太币的所有权,以及对合约进行控制。
在演示如何从私钥生成公钥之前,我们来看看椭圆曲线的细节。
椭圆曲线密码学的基本概念
椭圆曲线密码学是基于离散对数问题的非对称密码学(也称为公钥密码学),它是基于椭圆曲线上点位的加法和乘法的不可逆特性。
以太坊使用跟比特币系统相同的椭圆曲线算法,称为secp256k1。
这样以太坊就可以直接使用比特币系统中的大量椭圆曲线函数库和相关的开发工具。
以太坊使用一条特定的椭圆曲线和一组数学常量,这是一个被称为secp256k1的标准,由NIST设定。secp256k1曲线由下列函数定义,这些函数生成了椭圆曲线:
y2 = (x3+7) over Fp
或
y2 mod p = (x3+7) mod p
mod p(素数的模)表示曲线位于素数阶p的有限域中,这也可以表示为Fp,其中的p=2256–232–29–28–27–26–24–1是一个非常大的素数。
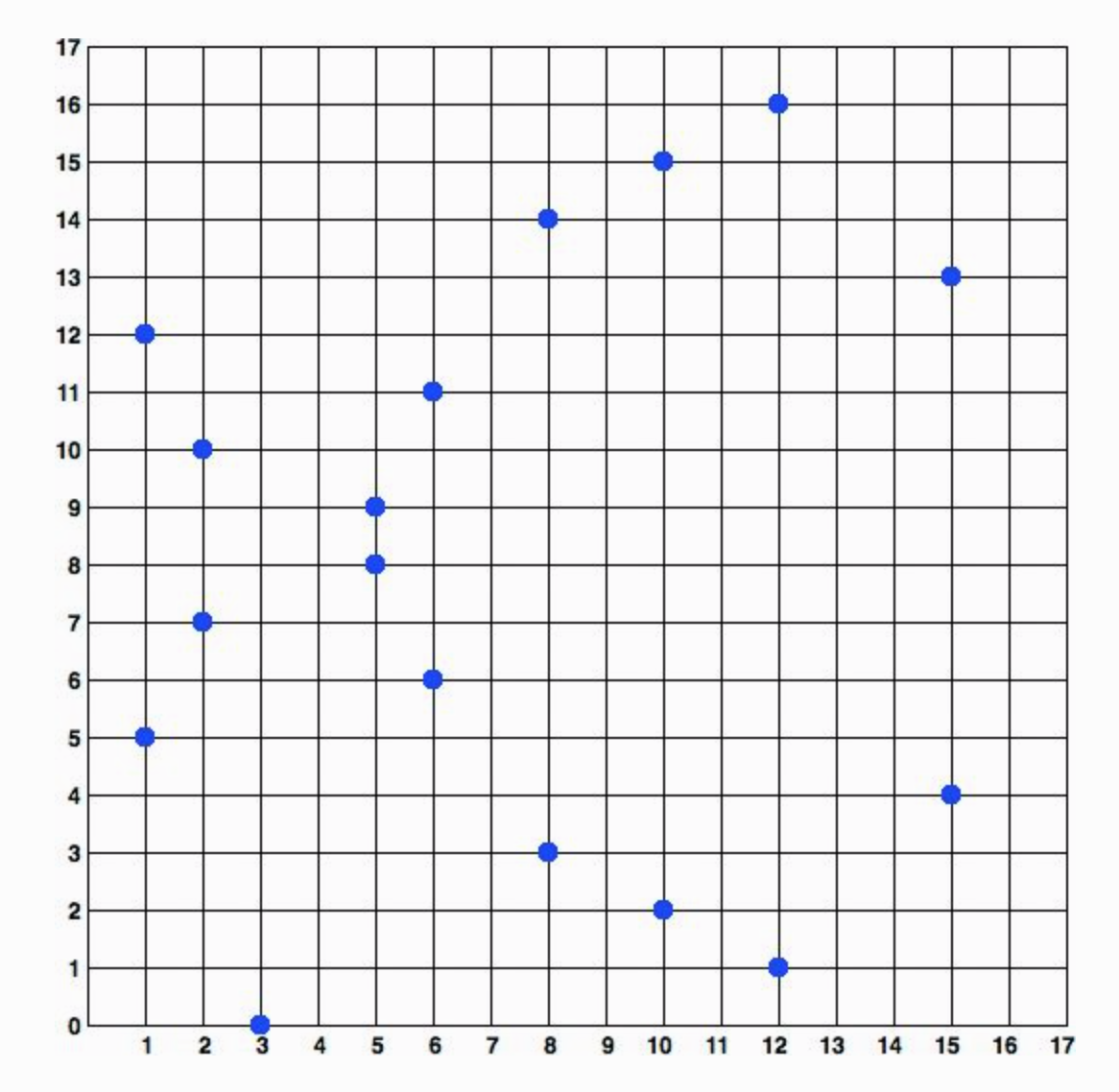
曲线的定义位于素数阶p的有限域中,而不是我们常见的实数空间。这个曲线的模式就像是散布在两个维度上的一组点,这是很难图形化表示的。然而,对于位于实数域的椭圆曲线,对应的算法也是一样的。例如,图3展示了同样一个位于有限域的椭圆曲线,但是它的素数阶(17)要小得多,显示为一个网格中的一系列点。椭圆曲线使用的secp256k1可以被认为是比这个复杂得多的模式,散布在一个巨大无比的网格之中。
例如,下面的Q点对应的(x,y)坐标是secp256k1曲线上的一个点位:
Q =
(49790390825249384486033144355916864607616083520101638681403973749255924539515,59574132161899900045862086493921015780032175291755807399284007721050341297360)
代码1演示了如何使用Python编程来检验这个点是否位于椭圆曲线上。变量x和y是Q点的坐标。变量p是椭圆曲线的素数阶(这个素数用来进行所有的求模计算)。Python代码的最后一行是椭圆曲线的等式(%运算符在Python中代表求模运算)。如果x和y的确是椭圆曲线上的点,那么它们就会满足方程,并且运算的结果是零(0L是一个零值长整数)。你可以自己编程尝试,通过Python的IDE,把下面的代码复制到»>提示符之后:
Python 3.4.0 (default, Mar 30 2014, 19:23:13)
[GCC 4.2.1 Compatible Apple LLVM 5.1 (clang-503.0.38)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> p = 115792089237316195423570985008687907853269984665640564039457584007908834 \
671663
>>> x = 49790390825249384486033144355916864607616083520101638681403973749255924539515
>>> y = 59574132161899900045862086493921015780032175291755807399284007721050341297360
>>> (x ** 3 + 7 - y**2) % p
0L
椭圆曲线上的运算
椭圆曲线的加法是两个点的相加
椭圆曲线上的很多数学运算看上去跟我们在学校学习的整数世界的数学运算类似。特别是,我们可以定义一个加法运算符,它并不是做数字之间的加法,而是把曲线上的两个点相加。有了加法运算符以后,我们还可以定义乘法运算符,用来在一个点和一个整数之间进行乘法运算,类似于重复进行加法运算。
椭圆曲线上加法运算的定义就是给定椭圆曲线上的两个点P1和P2,椭圆曲线上存在第三个点,满足P3=P1+P2。
从几何学的意义上来说,第三个点的计算其实是在P1和P2之间画一条线。这条线会与椭圆曲线存在唯一的相交点(超神奇),这个点称为P3’=(x,y),对应着在x轴我们就可以得到P3=(x,-y)。
如果P1和P2是同一点,那么P1和P2之间的这条线就应该是椭圆曲线上P1(P2)点的切线。这条切线会跟椭圆曲线存在唯一的相交点。你可以通过微积分的方式来确定这条切线的斜率。这样的计算是真的可以产出结果的,即使我们只有曲线上的两个坐标,仍旧可以算出对应的切线斜率。
椭圆曲线的无限远点在加法中的作用和我们平时所用加法中的0类似
在椭圆曲线的数学运算中,存在一个“无限远点”,这个点类似常规数学中的零。在计算机中,它有时被表述为x=y=0(这并不满足椭圆曲线的方程,但这是一个很容易验证的例子)。有一些特殊的案例可以用来解释为什么我们需要这个无限远点。
在一些情况下(比如P1和P2有相同的x值,却有不同的y值),那么两点的连线就是一条垂直的直线,这样的情况下,P3就是无限远点。
如果P1是无限远点,那么P1+P2=P2。同样,如果P2是无限远点,那么P1+P2=P1。这个例子展示了“无限远点”如何扮演着普通数学中零的作用。
这意味着,加法是满足结合律的,也就是说(A+B)+C=A+(B+C)。这意味着我们可以直接写A+B+C,即使不用圆括号,也不会产生运算上的歧义。
我们已经定义了加法,现在可以借此延伸出乘法的定义。对于椭圆曲线上的P点,如果k是一个整数,那么k*P=P+P+P+…+P(相加k次)。注意,有时候k会被称为“指数”,这比较容易令人混淆。
生成公钥
我们从随机得来的私钥k开始,使用椭圆曲线上预先定义好的名为生成点的G点来产生另一个位于椭圆曲线上的点,这就是对应的公钥K。
K=k*G
生成点由secp256k1椭圆曲线标准定义,在所有的secp256k1实现中,这个点保持不变,所有从这个曲线产生的公钥都是经过相同的生成点计算而来的。因为对于所有的以太坊用户而言,生成点始终保持不变,所以使用一个私钥k与生成点G计算之后,总是会得出相同的公钥K。k和K之间的关系是固定的,但是只能从一个方向进行计算,也就是通过k算出K。这也是为什么一个以太坊地址(从公钥K而来)可以被公开分享,而不用担心对应的私钥(k)可能会被人反向算出。
如同我们在上一节中提到的,k*G的乘法运算相当于是重复多次的加法运算,也就是G+G+G+…+G,重复k次。概括而言,为了从私钥k计算出公钥K,我们需要把生成点G反复相加k次。
通过私钥可以推算出公钥,但是通过公钥无法反向计算得出私钥,因为这个数学算法是单向的。
现在,让我们把这项计算用在之前“私钥”一节中生成的那个私钥,并通过这个私钥来计算得出公钥:
K = f8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315 * G
一些密码学类库可以帮助我们使用椭圆曲线加法来计算K。计算所得的公钥K定义为一个点:
K=(x,y)
其中:
x = 6e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b
y = 83b5c38e5e2b0c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0
在以太坊协议中,你可能会看到采用130个十六进制字符(65字节)表示的公钥。这是由SECG所发布的行业标准的一种序列化编码方式,在高效密码学标准(SECI)中有文献记载(http://www.secg.org/sec1-v2.pdf)这个标准定义了四种可能的前缀用来标示椭圆曲线上的点位,见表1。
| 前缀 | 含义 | 长度(以字节记) |
|---|---|---|
| 0x00 | 无穷远点 | 1 |
| 0x04 | 未压缩点 | 65 |
| 0x01 | 偶数y压缩的点 | 33 |
| 0x03 | 奇数y压缩的点 | 33 |
以太坊只使用未压缩的公钥,因此唯一相关的前缀就是0x04。包括x和y坐标的公钥经过编码后的形态如下:
04 + x-coordinate (32 bytes/64 hex) + y-coordinate (32 bytes/64 hex)
因此,我们在上文计算得出的公钥,经过编码后的形态为:
046e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b83b5c38e5e2b0 \
c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0